Avem o problemă de matematică cu o sumă a lui Gauss. Deși aceste tipuri de exerciții se învață în clasa a V-a, mulți adulți se încurcă în rezolvare. pentru a o face și mai dificilă vă provocăm să dați răspunsul în 15 secunde.
Doar cei cu adevărat inteligenți pot.
Problemă de matematică de clasa a V-a. Rezolvați rapid această sumă a lui Gauss. Accepți provocarea?
Suma Gauss este un concept matematic numit după un genial matematician german, Johann Karl Friedrich Gauss. Este cunoscut drept unul dintre cei mai influenți gânditori de matematică din istorie.
Citește și: Problemă de matematică. 16 ÷ 2 + 3 x 4=? Apoi citiți mai jos ce semnificație are numărul rezultat
Există o poveste faimoasă despre el care spune că a venit cu un mod inteligent de a aduna numere când era foarte tânăr. Profesorul lui de matematică a cerut odată clasei să adune toate numerele de la 1 la 100.
Sunt multe numere de adăugat unul câte unul, nu? Profesorul a crezut probabil că va dura mult, dar tânărul Gauss a avut un răspuns rapid: 5050, potrivit fresherslive.com.
Acum, povestea s-ar putea să nu fie în întregime adevărată, dar ne reamintește că uneori tinerii studenți pot descoperi noi idei de matematică. Gauss a găsit o modalitate inteligentă de a grupa numerele de la 1 la 100 pentru a le face mai ușor să le adunăm. Să examinăm o problemă pentru a înțelege cum funcționează acest truc de grupare.
Doriți să adăugați numerele de la 1 la 10
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = ?
Deci, gândiți-vă la rezolvarea puzzle-ului matematic așa cum a făcut Gauss.
Citește și: Problemă de matematică. Rezolvă rapid 10 - 2 x (4 ÷ 2) + 5=? Află semnificația numărului rezultat
Puteți rezolva aceste Gauss însumând numerele de la 1 la 10?
Dacă doriți să adăugați numerele de la 1 la 10. Puteți face acest lucru prin împerecherea numerelor. Mai întâi, adaugă primul număr cu ultimul număr, deci 1 + 10. Apoi, adaugă al doilea număr cu al doilea număr, care este 2 + 9. Continuă să urmezi acest model.
Deci tu ai:
(1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = ?
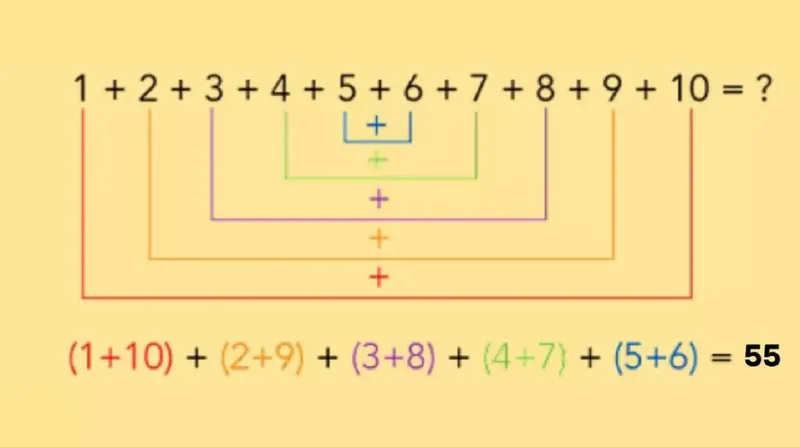
Foto: twitter/StummerVogel
Fiecare dintre aceste perechi adună până la 11. Deci, vă puteți gândi la problema noastră astfel:
(11) + (11) + (11) + (11) + (11) = ?
Deoarece avem 5 perechi, răspunsul nostru este:
11 + 11 + 11 + 11 + 11 = 11 x 5 = 55
Încercați următoarea metodă. În loc să puneți numerele pe un rând, le puteți aranja pe două rânduri. În primul rând, numerele cresc de la 1 la 10. În al doilea rând, numerele coboară de la 10 la 1. Când însumați fiecare coloană, obțineți 11 pentru fiecare coloană. Pentru a afla suma totală a tuturor numerelor, puteți înmulți numărul de perechi cu suma fiecărei perechi. Dar vrem doar suma unui rând, nu a ambelor rânduri. Deci, împărțim răspunsul nostru la 2.
Citește și: Problema de geometrie care se poate rezolva în 4 minute: ”Câte triunghiuri sunt?” Le poți număra?
Iată formula: Sumă totală = (număr de perechi x suma de perechi) / 2. Pentru cazul nostru, este (10 x 11) / 2, care este egal cu 55. Încercați această altă metodă pentru a aduna numere
. În algebră, putem reprezenta acest model folosind litera „n” pentru a reprezenta câte numere sunt în lista noastră. Pentru exemplul nostru, „n” este 10. Numărul de perechi este „n” împărțit la 2. Veți observa că dimensiunea perechii este numărul de perechi plus 1. Deci, îl putem scrie ca:
(numărul de perechi) x (suma fiecărei perechi) = (n/2) x (n + 1), care este egal cu (10 x 11) / 2, care este, de asemenea, egal cu 55.

































